Time window assignment and symmetry

In my previous blog post, I wrote about the problem of assigning time windows to clients, and I motivated why this is a relevant problem: nobody wants to wait at home all day because the delivery company said they would deliver between 9h and 17h. Today I would like to dive into a more technical aspect of assigning time windows, which is how symmetry negatively affects the methods that we use to find good time window schedules, and what we can do about that. In this blog post, I will sketch the basic idea with non-technical language. For a proper academic treatment, I refer to my joint work with prof. Guy Desaulniers, which will be published on this site soon.
To illustrate the problem of symmetry, let's consider the time window assignment problem pictured below. We are given five clients (A, B, C, D and E) who should all be served either in the morning, in the afternoon, or in the evening. The clients with blue circles (A, B, C and E) have to be visited by the blue truck. The clients with red squares (A,C, D and E) have to be visited by the red truck. Note that A, C and E have to be visited by both trucks. This means that if we assign a time window to, for example, client C, then both trucks should visit client C within that time window.
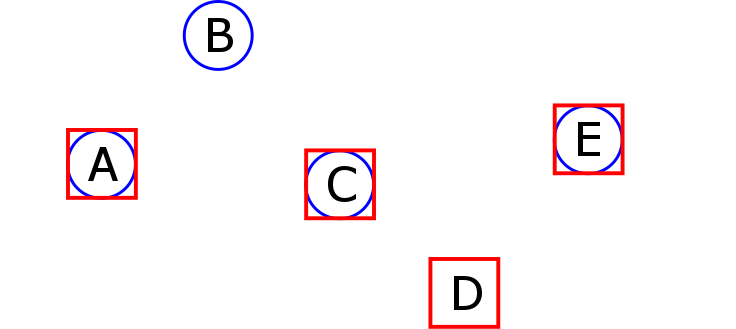
The most popular methods to solve problems like this are based on the "divide and conquer" strategy: the problem is split into multiple smaller and easier subproblems, which can again be split into even smaller and easier subsubproblems, etc., etc. Let's follow the same strategy, and split our problem into two smaller subproblems. In subproblem 1, we require that client A is visited in the morning. In subproblem 2, we require that client A is not visited in the morning. We give our two subproblems to some blackbox solver, and the following optimal solutions come out:
Solution subproblem 1 (client A visited in the morning):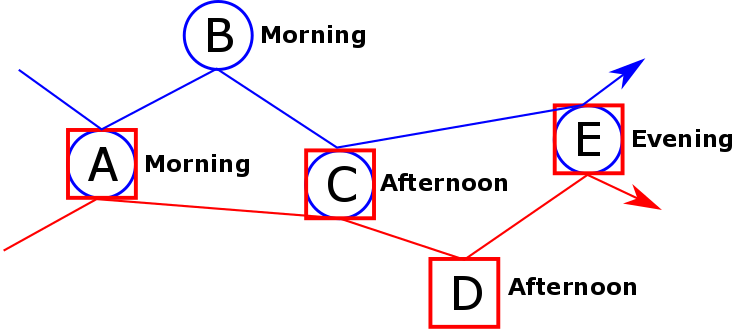
Solution subproblem 2 (client A not visited in the morning):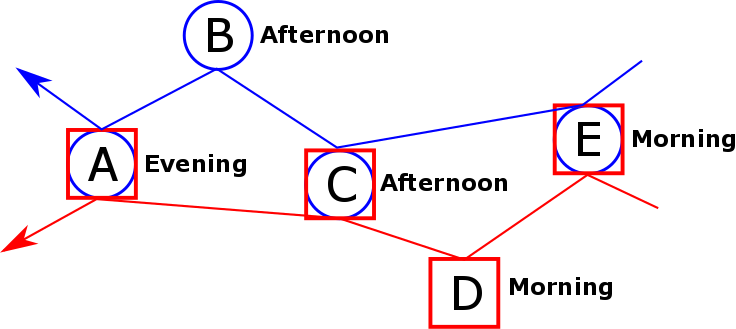
The blue and red arrows give the routes of the blue truck and the red truck, respectively. The assigned time windows are written next to the clients. So in the solution of subproblem 2, we see that the red truck visits E and then D in the morning, C in the afternoon, and finally A in the evening.
The important thing to notice is that the solutions to subproblem 1 and subproblem 2 are very similar. In both solutions, the trucks travel the exact same roads, just in different directions. Solutions like this are referred to as symmetric solutions. In hindsight, it would have taken less time to compute only one of these symmetric solutions, and then reverse the directions of the routes ourselves to find the other one. In other words, due to symmetry, we did twice the work we had to do.
How to deal with this symmetry? The basic idea is not complicated: we only split the problem (and subproblems, and subsubproblems, etc.) in such a way that we do not introduce symmetries. How to do this is detailed in our paper. The split in the example above (visiting client A in the morning / not visiting client A in the morning) is not allowed, as it could result in symmetric solutions, as we have just seen.
We applied this strategy to the problem of assigning time windows under demand uncertainty (i.e., when it is uncertain how many products clients will order), and there we saw that our method became a lot faster. Furthermore, we were able to assign time windows to more clients at the same time than ever before.
The reason for these results is that each split can introduce new symmetries. After one split, there may be 2 symmetric solutions, after two splits there may be 4, then 8, then 16, etc. By preventing these symmetries we thus avoid a huge amount of extra work. For one case, the amount of work was even reduced by over 500 times, which allowed us to find the optimal time window assignment, even though we were unable to do that before.
It is clear that handling symmetry in a correct way improves our methods for this specific problem, and the same idea may be relevant for related routing problems as well.
Key takeaways
When assigning time windows, symmetry causes unnecessary extra work.
Symmetry can be dealt with by changing how problems are split in smaller problems.
In the case of assigning time windows under demand uncertainty, it becomes easier to assign time windows when we appropriately deal with symmetry.
The same idea may be relevant for related routing problems.

