What is QCA?
(A more comprehensice comparison between NCA and QCA is here)
Qualitative Comparative Analysis (QCA; Ragin 1987, 2000, 2008, see also http://www.compasss.org/) is a method for identifying necessary and sufficient conditions using fuzzy sets. Condition X and outcome Y are expressed in terms of set membership scores, rather than conventional variable scores. With respect to a certain characteristic a case can be fully out of the set (set membership score = 0) or fully in the set (set membership score = 1). For example, the Netherlands is a case (of all countries) that can be considered as “fully in the set” of rich countries (based on the economic variable Gross Domestic Product, GDP), and Ethiopia can be considered as a case that is “fully out of the set” of rich countries. In crisp-set QCA (csQCA) the set membership scores can only be 0 and 1. In fuzzy-set QCA the membership scores can also have values between 0 and 1. For example, Croatia could be allocated a set membership score of 0.7 indicating that it is “more in the set” than “out of the set” of rich countries.
Set membership scores are obtained by transforming variable data and other information into set membership scores. This transformation process is called “calibration”. Calibration can be based on the distribution of the data, the measurement scale, or expert knowledge. Users of QCA can evaluate the (potentially large) effect of calibration on necessity using calibration evaluation tool.
QCA performs two separate analyses: a necessity analysis for identifying necessary conditions, and a truth table analysis for identifying sufficient configurations.
Necessity analysis of QCA compared to NCA
Although in most NCA applications conventional variable scores are used for quantifying condition X and outcome Y, NCA can also employ set membership scores for the conditions and the outcome, allowing a comparison between NCA and QCA. CsQCA and fsQCA have different procedures for identifying necessary conditions.
Necessity analysis of csQCA compared to NCA
The necessity analysis of csQCA is basically the same as NCA’s necessity analysis for dichotomous scores of X and Y. A necessary condition is assumed to exist if the condition is present (X=1) in virtually all cases where the outcome is present (Y=1), hence virtually no cases exist in which the outcome is present (Y=1) and the condition is absent (X=0). This is illustrated with the contingency table (see figure).
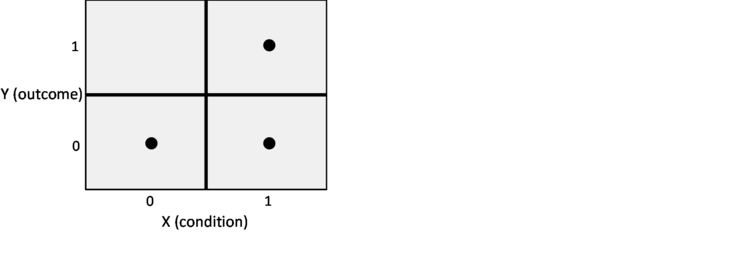
Both QCA and NCA assume that a necessary condition is plausible (with adequate theoretical support) if the upper left corner of the contingency table is virtually empty. QCA accepts a few cases (“deviant cases”) in the upper left corner. In csQCA necessary consistency is defined as the number of cases with the condition and the outcome present (the number of cases in the upper right corner) as a fraction of the total number of cases where the outcome is present (the total number of cases in the upper row). With a recommended consistency level of 0.9, csQCA accepts a maximum of 10% of cases with the outcome present in the “empty” upper left corner (where the condition is absent, contrary to necessity evidence). In NCA no rule is set for the “acceptable” number of cases in the “empty” cell, although a value 5% of the total number of cases has been suggested as an indication (95% accuracy). If no cases are allowed in the empty space (upper left corner), the results of the necessity analysis with csQCA and with NCA are the same. CsQCA’s necessity analysis can be considered as a special case of NCA (an NCA analysis with dichotomous, crisp set membership scores for X and Y, and an allowance of a specific number of cases in the empty zone given by the necessity consistency threshold).
Necessity analysis of fsQCA compared to NCA
The necessity analysis of fsQCA is different than the NCA’s necessity analysis for discrete or continuous scores of X and Y (Dul, 2016a; Vis and Dul, 2016). In fsQCA a necessary condition is assumed to exist if the area above the diagonal reference line in an XY scatter plot is virtually empty (see left figure).
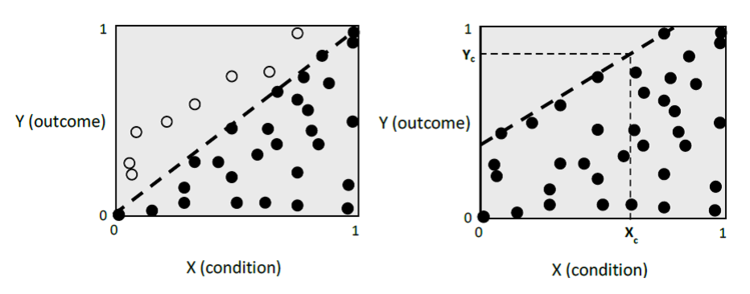
When cases are present in the “empty” zone above the diagonal (open circles) fsQCA considers these cases as “deviant cases”. FsQCA accepts some deviant cases as long as the necessity consistency level, which is computed from the total vertical distances of the deviant cases to the diagonal, is not smaller than a certain threshold, usually 0.9. FsQCA makes a qualitative (“in kind”) statement about the necessity of X for Y: “X is necessary for Y” (e.g., the presence of X is necessary for the presence of Y).
In contrast, NCA uses the ceiling line as the reference line (see right figure) for evaluating the necessity of X for Y (with possibly some cases above the ceiling line; accuracy below 100%). In situations where fsQCA observes “deviant cases”, NCA includes these cases in the analysis by moving the reference line from the diagonal position to the boundary between the zone with cases and the zone without cases. NCA considers cases around the ceiling line (and usually above the diagonal) as “best practice” cases rather than “deviant” cases. These cases are able to reach a high level of outcome (e.g., an output that is desired) for a relatively low level of condition (e.g., an input that requires effort).
In NCA the size of the “empty” zone as a fraction of the total zone (empty plus full zone) is called the necessity effect size. If the effect size is greater than zero (an empty zone is present) NCA has identified a necessary condition “in kind” that can be formulated as: “X is necessary for Y”, indicating that for at least a part of the range of X and the range of Y a certain level of X is necessary for a certain level of Y.
Additionally, NCA can quantitatively formulate necessary condition “in degree” by using the ceiling line: “level Xc of X is necessary for level Yc of Y”. The ceiling line represents all combinations X and Y where X is necessary for Y. (Although also fsQCA’s diagonal reference line allows for making quantitative necessary conditions statements, e.g. X>0.3 is necessary for Y=0.3, fsQCA does not make such statements).
When the ceiling line coincides with the diagonal (corresponding to the situation that fsQCA considers) the statement “X is necessary for Y” applies to all X-levels [0,1] and all Y-levels [0,1] and the results of the qualitative necessity analysis of fsQCA and NCA are the same. When the ceiling line is positioned above the diagonal “X is necessary for Y” only applies to a specific range of X and a specific range of Y. Outside these ranges X is not necessary for Y (“inefficiency”). Then the results of the qualitative necessity analysis of fsQCA and NCA can be different.
Normally, NCA identifies more necessary conditions than fsQCA. In the example NCA identifies that X is necessary for Y because there is an empty zone above the ceiling line. For example, for reaching an outcome level of Yc = 0.8 the necessary level of the condition is Xc = 0.6. Thus, when the condition level is below 0.6, it is not possible to reach an outcome level of 0.8. However, fsQCA would conclude that X is not necessary for Y, because the necessity consistency level is too small in this example (<0.9).
FsQCA’s necessity analysis can be considered as a special case of NCA (an NCA analysis with discrete or continuous fuzzy set membership scores for X and Y, a ceiling line that is diagonal, an allowance of a specific number of cases in the empty zone given by the necessity consistency threshold, and the formulation of a qualitative “in kind” necessity statement).
Sufficiency analysis of QCA
Although QCA can perform a necessity analysis as shown above, most QCA researchers focus on the sufficiency analysis. Whereas single necessary conditions are not uncommon (and very relevant because when the necessary levels of the condition are not in place the outcome will not occur), single sufficient conditions are extremely rare (in multicausal phenomena no single condition can produce the outcome). Therefore QCA focuses on combinations of conditions that are sufficient for the outcome (sufficient configurations). For identifying sufficient configurations QCA uses binary logic (using a truth table where the condition and outcome can have only two values: true of false). With k conditions of two values, a total of 2k possible combinations can be formulated. QCA identifies which of these combinations are observed in cases. Usually several configurations that can produce the outcome are observed(“equifinality”). When identified configurations are parsimonious (non-rerdundant) causal interpretations may be possible (Baumgartner, 2015).
QCA’s logical statements are expressed for example as follows (adapted from Goertz, 2003):
Y = X1*X2*X3 + X4*X5 (1)
In this example five conditions (X1, X2, X3, X4, X5) and one outcome Y are present. The symbol “+” means the logical “OR” and the symbol “*” means the logical “AND.” Equation (1) indicates that the presence of Y can be achieved via only two paths. The first paths is configuration X1*X2*X3 (the presence of X1 AND X2 AND X3) and the second possible path is configuration X4*X5 (the presence of X4 AND X5).
Each configuration has certain conditions (e.g., X1, X2,... ) that must be part of the configuration such that the configuration can produce the outcome. For example, X3 is part of the first configuration that can produce the outcome. The necessary parts of an outcome producing configuration are called INUS conditions (Mackie,1965): “Insufficient but Non-redundant (i.e., Necessary) part of an Unnecessary but Sufficient condition.” Non-redundant means that the conditions that are part of the configuration that produces (is sufficient for) the outcome, are essential (necessary).
Mackie (1965) repeatedly makes a distinction between an INUS condition and a necessary condition. For example he states on page 253: "Again, some causal statements pick out something that is not only an INUS condition but also a necessary condition". An INUS condition is only necessary for a specific configuration (non-redundant part of it), whereas a necessary condition is necessary for the outcome (hence must be present in all configurations that can produce the outcome). In equation (1) X3 is an INUS condition that is necessary for the configuration to produce the outcome, but it is not necessary for the outcome because configuration X4*X5 can also produce the outcome and does not contain X3. In contrast, in equation (2) below, where Y can be produced by only two configurations (X1*X2*X3 or X4*X3), X3 is part of both configurations that can produce the outcome.
Y = X1*X2*X3 + X4*X3 (2)
In equation (2) X3 is not only an INUS conditions for the two configurations, but also a necessary condition for the outcome. A condition is necessary if it is present in all configurations that produce the outcome. Normally, an INUS condition is not a necessary condition, but a necessary condition is always an INUS condition. Or as Mackie (1965, p. 253) puts it: "... some causal statements pick out something that is not only an INUS condition, but also a necessary condition."
It is possible that no necessary condition exist in the causal structure, but that only INUS conditions exist. For example in equation (1) there is no necessary condition and five INUS conditions. However, when a necessary condition is identified its practical relevance is clear-cut: if the condition is not in place in any possible configurations, the configuration will not produce the outcome. When the outcome is desired (e.g., performance in business applications) a practitioner must ensure that the necessary condition is always present. When the outcome is undesired (e.g., disease in medical applications) the practitioner must ensure that the necessary condition is never present (see NOTE below).
NCA is a method for identifying necessary conditions (hence its name). It is not designed for identifying sufficient configurations, nor for identifying INUS conditions of sufficient configurations. NCA only identifies necessary conditions for the outcome. These necessary conditions must be part of all sufficient configurations (and therefore become also INUS conditions for the configurations: insufficient but necessary parts of all unnecessary sufficient configurations).
NOTE: In his influential work on causes in epidemiological research, Rothman (1976) introduces the notion component causes of disease, which corresponds to Mackie’s INUS logic. “If there exists a component cause which is a member of every sufficient cause, such a component is termed a necessary cause. Necessary causes are often identifiable as part of the definition of effect” (p. 588, emphasis added). For example, certain bacteria and viruses are dichotomous necessary causes of infectious diseases: the tubercle bacillus is a necessary cause of tuberculosis, the Human Immunodeficiency Virus (HIV) is a necessary cause of AIDS, and the Human Papilloma Virus (HPV) is a necessary cause of cervical cancer (Dul, 2016b). Rothman et al. (2008) refer to a necessary cause (i.e., component cause of all sufficient causes) as a “universally necessary cause”. Prevention then can focus on the necessary cause (e.g., HPV screening and vaccination of women for prevention of cervical cancer).
Necessary condition versus necessary cause
Conditional statements are not the same as causal statements. According to the logic of conditional statements “A is necessary for B”, is equivalent to the conditional statements: “not A is sufficient for not B”, “B is sufficient for A”, and “not B is necessary for not A”. For example, when A is HIV and B is AIDS the following logical conditional statements apply if HIV is necessary for AIDS:
- HIV is necessary for AIDS
- No HIV is sufficient for no AIDS
- AIDS is sufficient for HIV
- No AIDS is necessary for no HIV
Conditional logic makes no assumption about the causal direction of the relationship between the concepts A and B. A fundamental difference between conditional statements and causal statements is that the latter presumes a temporal order between the concepts: first the cause (antecedent), then the effect (consequent). An infection of HIV precedes the disease AIDS (A causes B). Then it is not possible that AIDS precedes HIV (B causes A). Therefore conditional statements 3 and 4 are no correct causal statements. Only conditional statements 1 and 2 reflect that HIV is a necessary cause of AIDS. Statement 1 is the necessity of presence formulation of the necessary cause and statement 2 is the sufficiency of absence formulation of the necessary cause (Dul 2016b).
When researchers use NCA and other data analysis techniques for building and testing theory they presume a causal relationship between concepts. A fundamental characteristic of any scientific theory is that causal relationships exist between the concepts of the theory. These causal relationships are represented by arrows in a conceptual model, and allow for making predictions, which is one main goal of theory in applied sciences (“there is nothing as practical as a good theory”). In the context of theory causal statements are named “propositions”, and in the context of theory building or testing empirical research they are called “hypotheses”. In a necessary condition theory it is known or presumed that the condition precedes the outcome. This is emphasized by using the convention “X” for the condition (the cause), and “Y” for the outcome (the effect). Hence, in the context of theory and theory building or testing research “X is a necessary condition for Y” means “the presence of X is a necessary cause for the presence of Y”.
Empirical data can provide support or not for a causal necessary condition relationship. If the data suggest that A is a necessary condition for B, with the researcher’s information that A precedes B it is plausible that A is a necessary cause of B. Then the alternative reverse causality that B is a sufficient cause of A is not plausible, as B does not precede A. In other words, although the data may also support that B is a sufficient condition for A, the researcher’s information on the causal direction excludes the possibility that B is a sufficient cause of A. Information about the causal direction can be obtained, for example, by using a (quasi) experimental research design (where the condition X changes before the outcome Y), by providing theoretical arguments for the causal direction X --> Y, or by process tracing of cases to evaluate whether condition X changes before outcome Y. This additional information for making causal interpretations is similar to the additional information that is needed for making causal interpretations of correlations and associations in regression analyses.
A researcher in the applied sciences who uses a tool for analysing empirical data for building or testing theory assumes causal directions between the concepts of interest (reflected in propositions), based on additional information. Researchers who use NCA's (or QCA's) necessity analyses, usually assume that the condition causes the outcome, hence that A or B is the antecedent condition (X) and the other one is the outcome Y that follows. If it is assumed that B (assigned Y) follows A (assigned X), the data suggest that A (X) is necessary cause of B (Y). However, if it were assumed that A (assigned Y) follows B (assigned X) then the data suggest that B (X) is a sufficient cause of A (Y).
References
Baumgartner, M. (2015). Parsimony and causality. Quality & Quantity, 49(2), 839-856.
Dul, J. (2016a). ‘‘Identifying single necessary conditions with NCA and fsQCA.’’ Journal of Business Research 69(4):1516-1523.
Dul, J. (2016b). Necessary Condition Analysis (NCA). Logic and methodology of “necessary but not sufficient” causality. Organizational Research Methods, 19(1), 10-52.
Goertz, G. (2003). The substantive importance of necessary condition hypotheses. Necessary conditions: Theory, methodology, and applications, 65-94.
Mackie, J. L. (1965). Causes and conditions. American philosophical quarterly, 2(4), 245-264.
Ragin, C.C. (1987). The comparative method: Moving beyond qualitative and quantitative strategies. Los Angeles: University of California Press.
Ragin, C. C. (2000). Fuzzy-set Social Science. Chicago: The University of Chicago Press.
Ragin, C. C. (2008). Redesigning Social Inquiry: Fuzzy Sets and Beyond. Chicago:University of Chicago Press.
Rothman, K. J. (1976). Causes. American Journal of Epidemiology, 104(6), 587-592.
Rothman, K. J., Greenland, S., Poole, C., & Lash, T. L. (2008). Causation and causal inference. In: Rothman, K. J., Greenland, S., & Lash, T. L. (Eds.). Modern epidemiology. Lippincott Williams & Wilkins.
Vis, B. & Dul, J. (2016). Analyzing relationships of necessity not just in kind but also in degree: Complementing fsQCA with NCA. Sociological Methods and Research (in press).

