How does NCA work?
Scatter plot
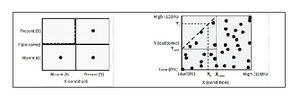
The starting point for identifying a necessary (but not sufficient) condition is a scatter plot of data (see figures). The scatter plot displays X values (X=condition) against Y values (Y=outcome). Each dot corresponds to one or more cases/observations. On the left the scatter plot is displayed as a contingency matrix where X and Y can only have two values (Absent/Present, or Low/High). This is a dichotomous necessary condition. On the right the X and Y can have any value within the Low and High limits. This is a continuous necessary condition.
Empty space
NCA searches for an empty space in the upper left-hand corner of the contingency table or scatter plot (with the convention that the X-axis is “horizontal” and the Y-axis is “vertical” and that values increase “upwards” and “to the right”). The empty space indicates that Y is constrained by X, and that X constrains Y.
Ceiling line
NCA draws a ceiling line between the empty space without cases/observations and the full zone with cases/observations (long dashed lines in the figures). This allows calculating the size of the empty space (“ceiling zone”).
Effect size
The effect size of a necessary condition is one of the major NCA parameters. The effect size is the relative size of the empty space compared to the entire space (“scope”). The larger the empty space compared to the rest of the observations, the larger the size of the necessary condition.
Necessary condition “in kind” and “in degree”
If the effect size d is large enough it can be stated that X is necessary for Y (qualitative or “in kind”). Furthermore, the (non-decreasing) ceiling line can be used to formulate a quantitative (“in degree”) necessary condition statement: level Y=Yc is only possible if level X≥ Xc (see right figure).
NCA software and NCA calculator
NCA software (in R) can be used to draw the ceiling line and calculate the effect size and other NCA parameters. The NCA calculator on this website can be used to get a quick calculation of the effect size.

