Frequently Asked Questions
This FAQ contains answers to questions concerning the following topics:
- Effect size calculations
- Meta-analytical techniques
- Confidence and prediction intervals
- Microsoft Excel and calculations
- Other topics
If your question is not included here, please contact us.
Effect size calculations
How can I meta-analyze regression coefficients?
You can’t / you shouldn’t. Several problems emerge with meta-analyses of regression coefficients, mostly caused by differences between the regression models. Specifically, a regression coefficient represents the effect of X on Y, controlled for other variables (Z). The problem that often occurs is that the variables included as controls differ between the studies. For example, a study on the effect of innovation on financial performance includes a control for firm size, but another study of the same relationship includes a control for prior financial performance. This way, the regression coefficient of the first study doesn’t represent the same effect as the coefficient from the second study.
The results of a regression model can be used to calculate so-called partial or semi-partial correlations (Aloë & Becker, 2012; Aloë, 2014). Therefore, two separate workbooks are included in the Meta-Essentials package: 6. Meta-Essentials Partial Correlational data; and 7. Meta-Essentials Semi-Partial Correlational data. The files can be used to calculate special types of correlation coefficients based on the information from regression models. For more information, see the text on effect sizes of the r-family in the User Manual.
Why do I need the correlation between pre- and post treatment in an experimental design with dependent groups?
We need to account for the correlation between pre- and post treatment ‘performance’, because we end up with a wrong estimate of the precision of the combined effect size (Morris & DeShon, 2002). The problem is that the groups in the experimental design are not independent of each other and we need some method to account for this dependence. In the independent groups design, i.e., with as separate treatment and control group, the correlation between the outcomes is by definition zero. However, when the correlation is not equal to zero, the variance of the difference between the group outcomes is over (or under) estimated.
Oftentimes, the correlation between outcomes is not known for the study of interest. Then, researchers need to make an informed decision (based on other studies) or make a sensitivity analysis by comparing the results for different levels of the correlation. See also section 4.2 of the User Manual and (Borenstein et al., 2009. p. 232).
What is the correct sample size (N) for experimental designs with dependent groups (within-subjects design)?
The total sample size (N) is the number of participants that participated in both the pre- and the posttest. And thus not the sum of participants in the pre- and posttest.
How can I calculate the standard error of the effect size if only z or t-statistics, or p-values are reported?
No problem! There are easy formulas you can use to derive the standard error of the effect size. See for example the online calculators of the Campbell Collaboration (based on Lipsey and Wilson, 2001): http://www.campbellcollaboration.org/resources/effect_size_input.php. Or Paul Ellis’s (2009) page: http://www.polyu.edu.hk/mm/effectsizefaqs/calculator/calculator.html. You can also use formulas in Microsoft Excel for inverting the t-distribution based on the p-values and the degrees of freedom: TINV(p;df). Remember from your statistics class that t = ES / SE.
The sign of the effect size is wrong / T-tests / F-tests from ANOVA
If the workbooks of Meta-Essentials calculate effect sizes based on t-value or F-values (from ANOVAs), then the calculated effect size sometimes needs to be negative. Oftentimes, articles present only absolute values of t or F, and then the correct sign of the effect must be interpreted from information reported elsewhere in the article, such as in the discussion of the hypothesis. If the effect should be negative, a minus-sign can be added to the t or F-value inserted in the input tab of the workbooks.
If the sign of the effect size is wrong for other reasons, please check if you inserted the information in the correct order (what is group 1, what is group 2?) and check for typos.
How to correct for statistical artifacts? Why do people quote Hunter & Schmidt (2004)?
Meta-analysts routinely correct for statistical artifacts as described in Hunter & Schmidt (2004), specifically when meta-analyzing correlation coefficients. Artifact corrections are proposed for reliability and imperfect construct validity, range restriction, and dichotomization of continuous variables. Researchers correct for these artifacts if they aim to provide a meta-analytical summary (i.e., combined effect size) of some relationship under ideal research circumstances. These corrections adjust the effect size upward (always) and this means the meta-analytical findings cannot easily be linked to any reported research finding.
The corrections can be applied before inserting the data (correlation coefficients) into workbook 5 of Meta-Essentials. This workbook does not provide automated calculation of adjusted effect sizes based on reliability estimates or other statistical artifacts. We emphasize that not everyone agrees such corrections are necessary (Lipsey & Wilson, 2001, p.109) and express our concern that only adjusting effect sizes upwards leads to unjustifiable large (and therefore likely statistically significant) combined effect sizes. Furthermore, insufficient data is often available from research reports to correct each effect size individually for their statistical artifacts, which is why many meta-analysts correct by using artifact distributions based on only the available data and assuming that this applies to data where it is unavailable as well.
Note that Hunter and Schmidt also propose different methods for meta-analyzing the effect sizes, but that Meta-Essentials follows the approach known as the Hedges-Olkin Meta-Analysis (HOMA).
Meta-analytical techniques
How many studies are required for a meta-analysis?
In theory, a meta-analysis should aim to provide a synthesis of all the studies in the theoretical domain, that is, all studies that provide an effect size relevant to your theory. Therefore, meta-analysts should aim to uncover any and all (including unpublished) studies.
Statistically speaking, at least two effect sizes are required to allow for the calculation of the confidence interval of the combined effect size, because it is based on a t-distribution with k-1 degrees of freedom. Also, each subgroup needs at least two effect sizes.
Unfortunately, there is no easy answer to this question as it depends on the field and the amount of research available for your theory. You should try to find as many studies as possible. Published meta-analyses in management often use data from somewhere between 50 and 300 articles and have used a range of methods to uncover all research.
Why do you assume a random effects model by default?
In Meta-Essentials the random effects model is used by default because the assumptions underlying the fixed effects model are very rarely met, especially in the social sciences. Furthermore, when a fixed effects model would make sense to use, i.e., when there is little variance in effect sizes, the random effects model automatically converges into a fixed effects model.
How to deal with dependent effect sizes, for example if the studies in the meta-analyses report on multiple outcomes or report multiple studies?
Some research reports present empirical evidence for multiple subgroups of a sample/population, or for multiple outcomes in a single study. These are essentially two different problems and therefore require different approaches. (See also: Borenstein et al., 2009: p. 215 ff).
Note that if a single study reports information for subgroups of the sample studied, these subgroups are essentially independent of each other, which means that the reported effect sizes for each of the subgroups can be treated as if they were separate studies.
Alternatively, and this does cause dependency problems in meta-analysis, a single study reports multiple outcomes for the same sample. For example, studies in management may report information on financial and non-financial performance, which for present purposes are both valid measures of the construct ‘performance’. The problem with this type of data is that the same units of analysis provided information for both outcomes, which means the effect sizes for both outcomes are not independent of each other, and incorrect estimates of the variance of the combined effect size will occur.
There are three approaches to this problem:
a. Select one of the reported effect sizes based on theoretical or pragmatic reasons, and ignore the other(s). A theoretical reason would be, for instance, that one of the effect sizes is a more valid measure of the concept you are interested in, compared to the other reported effect size(s). E.g., you theoretically argue that 'financial performance' is more valid measure of 'performance' than 'non-financial' performance. A pragmatic reason would be, for instance, that one of the reported effect size shows greater resemblance to other effect sizes already included in the meta-analysis. E.g., if most studies included in the meta-analysis operationalize ‘performance’ as ‘financial performance’, then this effect size is more comparable to the effect size from the other studies and may therefore be selected to include in the meta-analysis.
b. Combine the reported effect sizes into one combined effect size. The combined score is simply the arithmetic average of both scores: CS = (Y1+Y2)/2. However, the variance of this combined score is more complex: Vcs = (V1+V2+2r*√V1*√V2)/4, where r is the correlation between both outcomes. If the variances of outcomes 1 and 2 are equal, this simplifies to: Vcs = V(1+r)/2. All formulas are derived from Borenstein et al. (2009: 227 ff). Now, the combined score with its variance is the input to the meta-analysis of ‘performance’.
c. Perform separate meta-analyses for both types of effect sizes. This is of particular interest if you have multiple effect sizes of each type. The most obvious way of doing this, is by conducting completely separate meta-analyses in multiple workbooks of Meta-Essentials.Another, possibly more convenient, way of doing this is by entering all studies in one meta-analysis, but coding the different types of effect sizes as subgroups. However, when doing this, it is necessary that in the tab for Subgroup analysis, the 'Within subgroup weighting' is set to either 'Fixed effects' or 'Random effects (Tau separate for subgroups)'. You should not use within subgroup weighting with Tau pooled over subgroups, as this would violate the independency criterion. Furthermore, the combined effect size (i.e., the combined effect size over subgroups) should not be interpreted when using this method, as again, independence between effect sizes is assumed. Thus, only the subgroup effect sizes can be interpreted and compared, under the condition that Tau (the random variance component) is not pooled over subgroups.
Confidence and prediction intervals
What is the difference between the confidence and prediction intervals of the combined effect size?
The Meta-Essentials software does not only generate a confidence interval for the combined effect size but additionally a ‘prediction interval’. Most other software for meta-analysis will not generate a prediction interval, although it is - in our view - the most essential outcome in a ‘random effects’ model, i.e. when it must be assumed that ‘true’ effect sizes vary. If a confidence level of 95% is chosen, the prediction interval gives the range in which, in 95% of the cases, the outcome of a future study will fall, assuming that the effect sizes are normally distributed (of both the included, and not (yet) included studies). This in contrast to the confidence interval, which “is often interpreted as indicating a range within which we can be 95% certain that the true effect lies. This statement is a loose interpretation, but is useful as a rough guide. The strictly-correct interpretation [… is that, i]f a study were repeated infinitely often, and on each occasion a 95% confidence interval calculated, then 95% of these intervals would contain the true effect.” (Schünemann, Oxman, Vist, Higgins, Deeks, Glasziou, & Guyatt, 2011, Section 12.4.1).
Why are the confidence intervals of the combined effect size in Meta-Essentials different than in other programs?
This has to to with the so-called ‘weighted variance method’ for estimating the confidence interval of the Combined Effect Size. We refer very briefly to this in a section of the User Manual. Sanchez-Meca and Marin-Martinez (2008) show that this weighted variance method outperforms other methods, such as a simple t-distribution or Quantile Approximation (and definitely the normal distribution).
Note that the ‘weighted variance method’ to estimate the CI of the Combined Effect Size is not to be confused with the ‘inverse variance weighting’ method used to estimate the Combined Effect Size itself!
Other programs use (or let the user choose between) a normal distribution or a t-distribution (CMA, MIX, OpenMeta[analyst], metafor). ESCI (Cumming, 2012) applies a non-central t-distribution, which is also an improvement over the more standard approached (Cumming & Finch, 2001).
Why is the confidence interval of the combined effect size sometimes larger than the confidence intervals of the individual effect sizes, specifically with a low number of studies?
The confidence interval of the combined effect size is based on a t-distribution with k-1 degrees of freedom, k being the number of effect sizes. Therefore, if k decreases, the critical t-value to base the confidence interval increases. This reflects that a small number of studies does not give much certainty about the precision of the combined effect size. With more studies comes more confidence in the precision of the combined effect size.
At first, this may seem counterintuitive as you would expect that the confidence interval of the combined effect size would always be smaller and therefore give more precision regarding the combined effect size (particularly when individual effect sizes are very similar, i.e., homogeneous). However, assuming 95% confidence level, the 95% CI represents that range in which we can expect the combined effect to fall when the studies would be executed again. The imprecision includes, but is not limited to, sampling error and between-studies variance.
Microsoft Excel and calculations
Do I need Microsoft Excel to use Meta-Essentials?
Not necessarily. Although we designed Meta-Essentials for Microsoft Excel, it also works with the freely available WPS Office 2016 Free and Microsoft Excel Online (free registration required). We are currently working on a version for LibreOffice.
In what version(s) of Microsoft Excel does Meta-Essentials run?
The workbooks of Meta-Essentials are compatible with Microsoft Excel 2010, 2013 and 2016. Older versions of Excel might work fine in some cases, but some formulas and formatting features are not supported by these older versions.
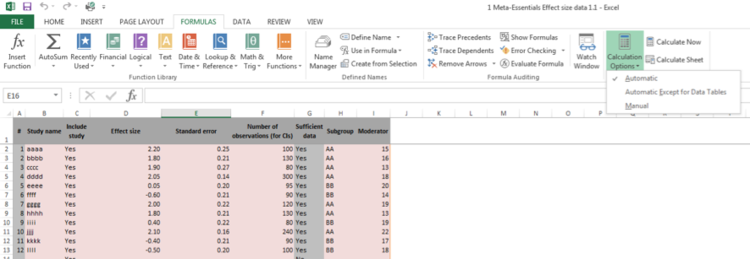
Why does it take so long to perform the calculations every time I insert new data?
The reason is that Excel recalculates every formula in the workbook each time a single new piece of data is inserted. To make your life easier, you can temporally set Excel to manually (and not automatically) calculate the workbooks, see the options in the ‘Formulas’ tab in the ribbon of Microsoft Excel. After you inserted all the data, you can either click ‘calculate now’ or set to automatically calculate.
Other topics
What is the source of the data in the workbooks?
All the data inserted by default in the workbooks of Meta-Essentials is fictitious and were purposefully chosen to display some of the key features of the workbooks, such as the subgroup analysis. Thus, all the effect sizes, standard errors, subgroup variables, and moderator variables, were chosen by us. This data should be deleted before you start your own meta-analysis.
What sources do you recommend to interested readers?
Textbooks on the entire process of a structured literature review:
- Cooper, H. (2009). Research synthesis and meta-analysis: A step-by-step approach (4th ed.). Los Angeles etc.: SAGE Publications.
- Lipsey, M. W., & Wilson, D. (2001). Practical meta-analysis. Thousand Oaks, London, New Delhi: SAGE Publications.
For more on the statistics behind meta-analysis:
- Borenstein, M., Hedges, L., Higgins, J. P. T., & Rothstein, H. R. (2009). Introduction to Meta-Analysis. Chichester, UK: John Wiley & Sons, Ltd.
- Cooper, H., Hedges, L. V., & Valentine, J. C. (Eds.). (2009). The Handbook of Research Synthesis and Meta-Analysis (2nd Edition). New York: Russel Sage Foundation.
- Higgins, J. P. T., & Green, S. (Eds.). (n.d.). Cochrane Handbook for Systematic Reviews of Interventions (version 5.1.0). The Cochrane Collaboration.
For more information on the (mis)use of p-values, the usefulness of CIs, etc:
- Cumming, G. (2012). Understanding the New Statistics. New York: Taylor & Francis Group.
- Cumming, G., & Finch, S. (2001). A Primer on the Understanding, Use, and Calculation of Confidence Intervals that are Based on Central and Noncentral Distributions. Educational and Psychological Measurement, 61(4), 532–574.
- Cumming, G. (2013, September 22). Dance of the p-values. [video file] Retrieved from: https://www.youtube.com/watch?v=5OL1RqHrZQ8
For more general information on effect sizes:
- Cumming, G. (n.d.) The New Statistics. [website] Retrieved from: http://www.thenewstatistics.com
- Ellis, P. (n.d.) Effect Size FAQs. [website] Retrieved from: https://effectsizefaq.com
How can I do more advanced meta-analyses?
There are several types of more advanced meta-analytical approaches that cannot be executed using Meta-Essentials. For example, the workbooks can only run a meta-regression for a single covariate and the subgroup analysis does not allow for multilevel structure, which are often applied in published meta-analyses. However, for exploratory analyses and educational purposes, Meta-Essentials provides a great introduction.
There is other software available if you are interested in such more advanced methods. For multi-level, network, and meta-regression, we suggest metafor, a meta-analysis package for R, (Viechtbauer, 2010). This package is freely available (as is R). For meta-analytical structural equation modeling the best approach is to use the study-level correlation matrices in a two-stage structural equation model, described in (Cheung & Chan, 2005; Cheung, 2015a) and also available in an R-package (meta-SEM; Cheung, 2015b).
How do I cite Meta-Essentials?
The preferred citation for use of the workbooks of Meta-Essentials can be found below. Please appropriately attribute your use of the tool to our original effort to develop it and provide it for free.
Furthermore, if you want to refer explicitly to the material in the user manual or the text on interpreting results, please cite these texts specifically as indicated on their respective home pages.
What has been changed in version 1.1 compared to 1.0?
Compared to version 1.0, version 1.1 only solved some bugs in the forest plot of the subgroup analysis (not all effect sizes were properly displayed).
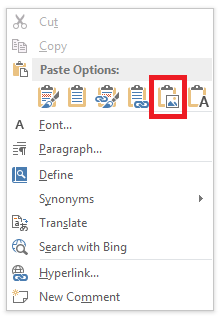
How do I use figures from Meta-Essentials in my research reports?
In the workbook, first adapt the layout of the content you would like to export to your preferences. Then, select the content you would like to export and press Ctrl + C (or right-click and select ‘Copy’). Go to Microsoft Word or Microsoft PowerPoint and right click where you want to insert the content and a menu as shown in the Figure below will appear. Under ‘Paste Options’, select ‘Picture’ (the option with the red box around it in the Figure below). That’s it.
Preferred citation
To cite the tools:
- Suurmond, R, van Rhee, H, & Hak, T. (2017). Introduction, comparison, and validation of Meta-Essentials: a free and simple tool for meta-analysis. Research Synthesis Methods. 1-17. doi.org/10.1002/jrsm.1260
To cite the user manual:
- Van Rhee, H.J., Suurmond, R., & Hak, T. (2015). User manual for Meta-Essentials: Workbooks for meta-analyses (Version 1.0) Rotterdam, The Netherlands: Erasmus Research Institute of Management. Retrieved from www.erim.eur.nl/research-support/meta-essentials
To cite the text on interpreting results from meta-analysis:
- Hak, T., Van Rhee, H. J., & Suurmond, R. (2016). How to interpret results of meta-analysis. (Version 1.0) Rotterdam, The Netherlands: Erasmus Rotterdam Institute of Management. Retrieved from: www.erim.eur.nl/research-support/meta-essentials
References
Aloë, A. M., & Becker, B. J. (2012). An Effect Size for Regression Predictors in Meta-Analysis. Journal of Educational and Behavioral Statistics, 37(2), 278–297. http://doi.org/10.3102/1076998610396901
Aloë, A. M. (2014). An Empirical Investigation of Partial Effect Sizes in Meta-Analysis of Correlational Data. The Journal of General Psychology, 141(1), 47–64. http://doi.org/10.1080/00221309.2013.853021
Borenstein, M., Hedges, L., Higgins, J. P. T., & Rothstein, H. R. (2009). Introduction to Meta-Analysis. Chichester, UK: John Wiley & Sons, Ltd. doi.org/10.1002/9780470743386
Cheung, M. W.-L. (2015). Meta-Analysis: A Structural Equation Modeling Approach. Chichester, UK: John Wiley & Sons, Ltd.
Cheung, M. W.-L., & Chan, W. (2005). Meta-analytic structural equation modeling: a two-stage approach. Psychological Methods. Retrieved from http://psycnet.apa.org/journals/met/10/1/40/
Cheung, M. W.-L. (2015). metaSEM: an R package for meta-analysis using structural equation modeling. Frontiers in Psychology, 5. doi.org/10.3389/fpsyg.2014.01521
Cumming, G. (2012). Understanding the New Statistics. New York: Taylor & Francis Group.
Cumming, G., & Finch, S. (2001). A Primer on the Understanding, Use, and Calculation of Confidence Intervals that are Based on Central and Noncentral Distributions. Educational and Psychological Measurement, 61(4), 532–574. http://doi.org/10.1177/0013164401614002
Hunter, J. E., & Schmidt, F. L. (2004). Methods of meta-analysis: correcting error and bias in research findings (2nd, April). Thousand Oaks, London, New Delhi: SAGE Publications.
Lipsey, M. W., & Wilson, D. (2001). Practical meta-analysis. Thousand Oaks, London, New Delhi: SAGE Publications.
Morris, S. B., & DeShon, R. P. (2002). Combining effect size estimates in meta-analysis with repeated measures and independent-groups designs. Psychological Methods, 7(1), 105–125. doi.org/10.1037//1082-989X.7.1.105
Sánchez-Meca, J., & Marín-Martínez, F. (2008). Confidence intervals for the overall effect size in random-effects meta-analysis. Psychological Methods, 13(1), 31–48. http://doi.org/10.1037/1082-989X.13.1.31
Schünemann, H., Oxman, A., et al. (2011). Interpreting results and drawing conclusions. In J. P. T. Higgins & S. G. Green (Eds.), Cochrane Handbook for Systematic Reviews of Interventions. The Cochrane Collaboration. Retrieved from https://training.cochrane.org/handbook
Viechtbauer, W. (2010). Conducting meta-analyses in R with the metafor package. Journal of Statistical Software, 36(3), 1–48. https://doi.org/10.1103/PhysRevB.91.121108


