Failsafe-N tests
The workbooks and a pdf-version of this user manual can be downloaded from here.
The final part of the Publication Bias Analysis sheet contains several estimates of Failsafe numbers. To illustrate this, imagine that for any study, a number of other studies is not published. Assume that these additional studies have insignificant results, i.e. their effect sizes are essentially zero. Then, the failsafe number estimates the number of such additional studies that are required to turn the effect size from the included and additional studies combined insignificant, i.e. that the ‘new’ combined effect size is essentially zero.
Rosenthal
In order to calculate a Failsafe-N, first described by Rosenthal (1979), a test of combined significance is conducted. The failsafe number is the number of missing studies averaging a z-value of zero that should be added to make the combined effect size statistically insignificant (see Figure 26 for an example). The ad-hoc rule refers to the one by Rosenthal (1979) for deciding whether the number estimated is small (TRUE) or large (FALSE).
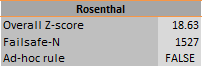
Figure 26: Example of Rosenthal’s Failsafe-N of the Publication Bias Analysis sheet
Gleser & Olkin
Gleser and Olkin (1996) provide an estimate for the number of unpublished results (see Figure 27 for an example). It uses the assumption that the studies in the meta-analysis have the largest significance (i.e., smallest p-values) from a population of effect sizes. The size of the largest p-value in the meta-analysis determines the number of estimated unpublished studies. There is no method to assess whether this number is small or large, but a comparison could be made with the number of studies that actually are included in the meta-analysis.

Figure 27: Example of Gleser and Olkin’s Failsafe-N of the Publication Bias Analysis sheet
Orwin
Orwin (1983) uses a slightly different approach by looking at effect sizes rather than at p-values. For this method, the user sets a criterion value for the combined effect size. The user can set any value that would make the result of the meta-analysis arbitrary (ESC) (see Figure 28 for an example). Secondly, the user sets the mean of the studies that are imputed (ESFS). Then the failsafe number will give the number of studies with average effect size (ESFS) that would reduce the combined effect to the criterion value (ESC).

Figure 28: Example of Orwin’s Failsafe-N of the Publication Bias Analysis sheet
Fisher
The fourth and final failsafe number method provided by Meta-Essentials (proposed by Fisher, 1932) is also based on a test of the combined significance (see Figure 29 for an example). It is based on the sum of the natural logarithm of the p-values from the studies in the meta-analysis. The number can be tested with a Chi-Square distribution with degrees of freedom of two times the number of studies in the meta-analysis.
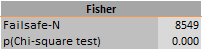
Figure 29: Example of Fisher’s Failsafe-N of the Publication Bias Analysis sheet
References
Fisher, R. A. (1932). Statistical methods for research workers (Fourth Ed.). Edinburgh, UK: Oliver & Boyd. www.worldcat.org/oclc/4971991
Gleser, L. J., & Olkin, I. (1996). Models for estimating the number of unpublished studies. Statistics in Medicine, 15(23), 2493-2507. dx.doi.org/10.1002/(sici)1097-0258(19961215)15:23%3C2493::aid-sim381%3E3.0.co;2-c
Orwin, R. G. (1983). A fail-safe N for effect size in meta-analysis. Journal of Educational Statistics, 8(2), 157-159. dx.doi.org/10.2307/1164923
Rosenthal, R. (1979). The file drawer problem and tolerance for null results. Psychological Bulletin, 86(3), 638-64. dx.doi.org/10.1037/0033-2909.86.3.638


